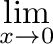Thesis Structure

Chapter II starts by reviewing some of the fundamentals in queueing theory upon which the approximations are based. The closure approximations are presented for the M/M/1 queue and compared to reveal differences in structure [#!ROPC:1!#].

In Chapter III the M/M/1 approximations are tested against exact methods for both stationary and nonstationary arrival patterns. The stationary cases are compared against exact results from Cantrell [#!JS:1!#,#!PR:1!#], while the nonstationary cases will be compared to solutions from Kolmogorov forward equations. Each approximation will be characterized to show areas of weakness and strength.

In Chapter IV the methods proving to be most accurate will be tested in a two node feed-forward network, otherwise known as the tandem queue. The results are compared against the Kolmogorov forward equation solutions and results from the previous chapter to see the effect of the first node on the accuracy of the second node results.

In Chapter V final conclusions are drawn and suggestions for further research topics are suggested. An equation using the equation environment

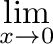$\displaystyle \lim_{{x\to0}}^{}$$\displaystyle {\sin x\over x}$ = 1, (1)
and one using the displaymath environment

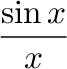$\displaystyle \sqrt{{1+\sqrt{1+\sqrt{1+x}}}}$.

are displayed here. Now refer to Fig. [*] for another example of what you can do with the LATEX picture environment.
Figure: Overall Structure
\begin{figure}\begin{center}\setlength{\unitlength}{1in} \begin{picture}(5,6)... ...,-1){1}} \put(2.5,2.25){\vector(0,-1){1}} \end{picture}\end{center} \end{figure}